CF1829G Hits Different 题解

蒟蒻在赛时把这题想得有点复杂了 QAQ（虽然也能 AC

先上个保险以免溢出。

1	`#define int long long // (1)`

来自很久之后作者的提醒：define 一个关键字是 UB，并且这是一个坏习惯。

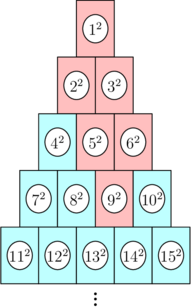
观察这张图，我们发现每层最左端的数可组成序列：

\[1^2,\ 2^2,\ 4^2,\ 7^2,\ 11^2,\ 16^2,\cdots\]

注意到，这些数的底数不就是二阶等差数串么：

\[1^2,\ (1+1)^2,\ (1+1+2)^2,\ (1+1+2+3)^2,\ (1+1+2+3+4)^2,\ (1+1+2+3+4+5)^2,\cdots\]

所以可以预处理出每层最左边的数。

constexpr static int Max=1e6+1;
vector<int>a;
void init()
{
    a.push_back(-1); // 占位
    int now=1,d=1;
    a.push_back(now);
    while(now<Max)
    {
        now+=d;
        ++d;
        if(now<Max)a.push_back(now);
    }
}

那么另一个需要解决的点就是如何推出上一层会掉落的纸杯，其实这个很简单，只要再观察一下就可得到如下的规律（下用 \(l(l>1)\) 表示当前层数）：

\[\mathrm{left}_{l-1} = \mathrm{left}_{l} - l\\ \mathrm{right}_{l-1} = \mathrm{right}_{l} - l + 1\]

注意左右端点可能会超出边界，所以还要分别取 \(\mathrm{max}\) 和 \(\mathrm{min}\)。

核心代码如下：

int n,l,ans;
int le,ri;
vector<int>::iterator w;
void solve()
{
    cin>>n;
    w=upper_bound(a.begin(),a.end(),n);
    l=w-a.begin()-1; // 注意 -1 才是当前层
    ans=n*n;
    le=ri=n;
    while(l)
    {
        le-=l, ri-=l-1;
        --l; // 到达上一层
        le=max(le,a[l]);
        ri=min(ri,a[l+1]-1);
        for(int i=le;i<=ri;i++)
            ans+=i*i;
    }
    cout<<ans<<endl;
}

完整代码如下：

// 珍爱账号，请勿贺题
#include <bits/stdc++.h>
using namespace std;
#define int long long

constexpr static int Max=1e6+1;
vector<int>a;
void init()
{
    a.push_back(-1);
    int now=1,d=1;
    a.push_back(now);
    while(now<Max)
    {
        now+=d;
        ++d;
        if(now<Max)a.push_back(now);
    }
}

int n,l,ans;
int le,ri;
vector<int>::iterator w;
void solve()
{
    cin>>n;
    w=upper_bound(a.begin(),a.end(),n);
    l=w-a.begin()-1;
    ans=n*n;
    le=ri=n;
    while(l)
    {
        le-=l, ri-=l-1;
        --l;
        le=max(le,a[l]);
        ri=min(ri,a[l+1]-1);
        for(int i=le;i<=ri;i++)
            ans+=i*i;
    }
    cout<<ans<<endl;
}

int T;
int32_t main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin>>T;
    init();
    while(T--)solve();

    return 0;
}

CF1829G Hits Different 题解

评论