AT_mujin_pc_2016_b ロボットアーム 题解

年代久远

您正在查看一篇年代久远的题解，由于 Markdown 格式不兼容等问题，页面渲染可能会出现问题。其中的时效性信息可能不再有效，请仔细辨别。

题面(洛谷)

题面(AtCoder)

AtCoder Problems 评级难度：958。

思路

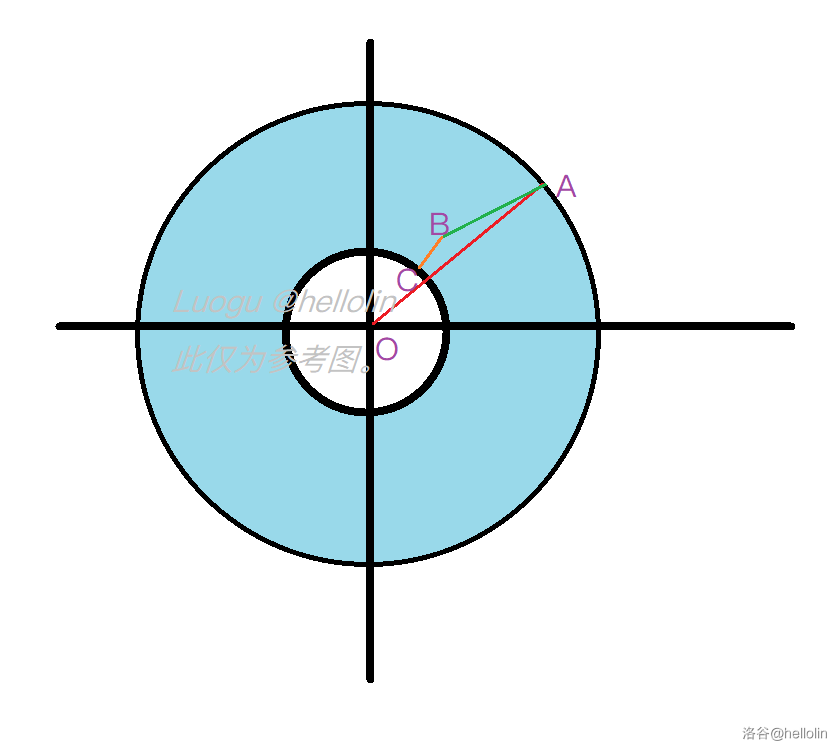
由样例解释图易知，求解的部分是是一个圆环（当小圆半径 \(r=0\) 时是一个整圆）。

首先需要会圆环的计算公式。（大概是小学内容）

\[S=\pi \cdot (R^2 - r^2)\]

大圆半径 \(R\) 不必多说，把手臂伸最长就是。

\[R=l_{OA}+l_{AB}+l_{BC}\]

小圆半径 \(r\) 求解如下：

由 \(l_{OC}=l_{OA}+l_{AB}+l_{BC}\) 易知，即使改变这三条线段的顺序，\(C\) 点的坐标和将会扫过的面积也不会改变。可将 \(OA\) 段改为最长的那段，此时将 \(OA\) 伸直，其余两段往回伸，扫一圈（见下图，手画画得丑见谅），小圆的半径就是 \(r=l_{OA}-(l_{AB}+l_{BC})\) 了。

整理如下（先进行排序使得 \(OA\ge AB\ge BC\)）：

\[S=\pi \cdot (R^2 - r^2)\]

\[R=l_{OA}+l_{AB}+l_{BC}\]

\[r=\left\{\begin{aligned}0\ (AB+BC\ge OA)\\OA-(AB+BC)\ (AB+BC< OA)\end{aligned}\right.\]

代码

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <cmath>
#define PI acos(-1)
int a[4];
double R, r;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin>>a[1]>>a[2]>>a[3];

    std::sort(a+1,a+4); // 排序，此时 a[3] 最大

    R = a[1]+a[2]+a[3];
    r = a[3]-(a[1]+a[2]);
    r = r<0?0:r;

    std::cout<<std::fixed<<std::setprecision(10);
    std::cout<<(PI*(R*R-r*r))<<std::endl;
    return 0;
}

评论